Have you ever heard of constant difference? You may know it or don’t but you have used it in real life even though you didn’t know it by name. Here we going to explain what is it? Why is it important? and everything we want you to know about it.
What is a constant difference?
The constant difference is referred to some kind of relationship between two variables. The difference between a couple of numbers does not change after adding or substracting both of them with the same number. This is a very simple mathematical concept but it can be used for many things. Before you going to know them you should have a better understanding of Constant differences.
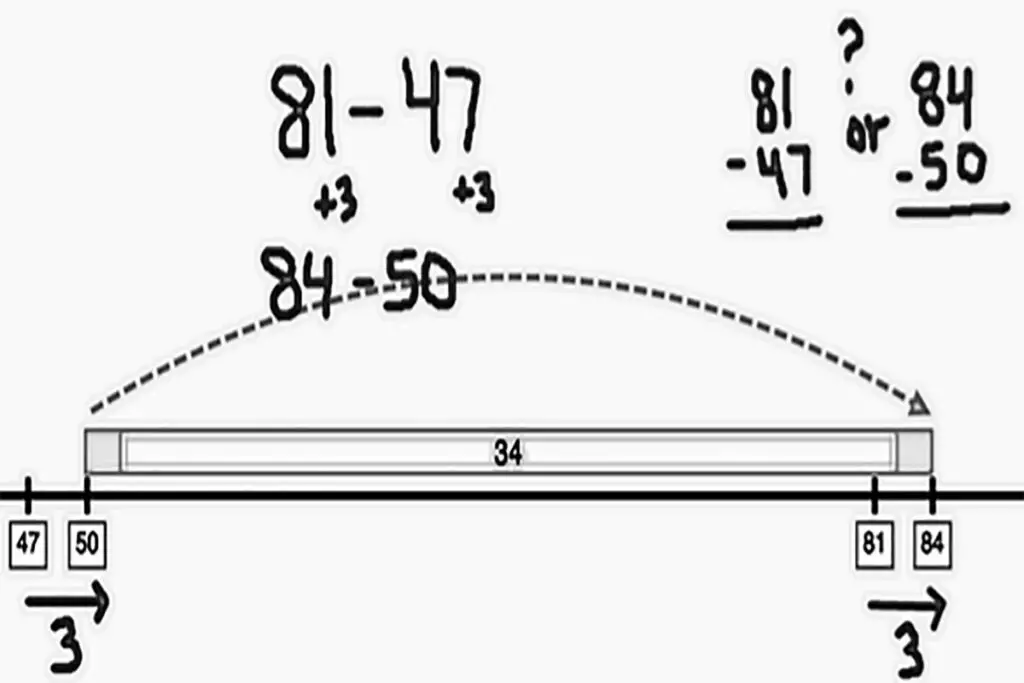
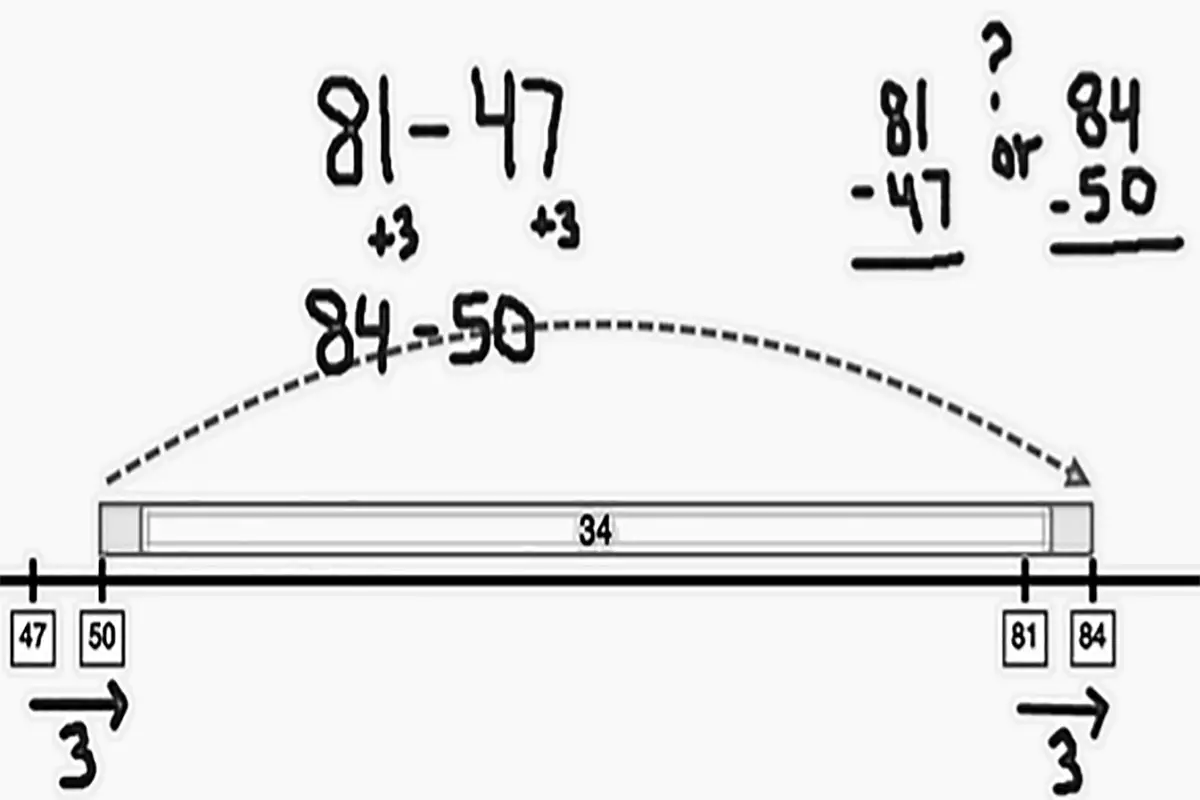
Understanding constant difference.
These images illustrate constant difference which is a trick that we can use to decide from a table of values whether we have a linear function that can be described with a straight line equation.
| X | Y |
| 1 | 8 |
| 2 | 16 |
| 3 | 24 |
| 4 | 32 |
| 5 | 40 |
All I have to do is take a larger y coordinate like this 16 and subtract a smaller y coordinate like the 8 and see what the difference is if I keep doing this. I keep getting the same answer. That’s the constant difference. 8 is the constant difference and this allows me to say with some confidence this looks like a linear relationship and I can go ahead and try to derive the linear equation that goes with it.
Sometimes you get perfect constant differences like this especially when the question was built for you by someone. Creating an equation using that equation to create a table of values then you get an exact constant difference of 8 in this case.
Experimental data
But some tables of values will be derived from experimental data and experimental data isn’t necessarily perfect. It’s not going to give you a perfect constant difference but it could be close enough. So, that you’re still able to say I think this is a linear relationship and then find a straight line equation that goes with it.
| X | Y |
| 0 | 10 |
| 2 | 19 |
| 4 | 30 |
| 6 | 41 |
| 7 | 46 |
Looking at this table of values I’m saying 19 – 10 = 9 and 30 – 19 = 11. It’s not the same difference 41 – 30 = 11. I’m getting a very similar answer in each case and I’m able to say this is close enough so that I can assume that this is a linear relationship and then I go ahead and I find the equation of the straight line that goes with it.
Watch out for situations like this because in this table of values the X values are going up by twos but then I have one where it just goes up by one. So instead of this going up by 11 or 10 or 9 close to 10, it’s going up by 5. It is still part of the same straight line relationship but you have to watch out for how your X values are changing.
Notice that I’m always using two consecutive points in the table when I do my subtractions if I just choose points at random I’m not going to be able to see the constant difference so the constant difference trick is very useful when looking at table values when you’re trying to decide what type of relationship exists between the X and the Y in the function.
Why is it important?
It supports some student learning strategies.
No one expects complex math from elementary students. However, there are few mathematical concepts they need to understand. To solve complex mathematical problems in the future, they should have a clear understanding of these concepts. Even though they are basic concepts, teaching them to a student can be hard. That’s why students should have thought about learning strategies.
In mathematics, throughout education and professional works, the relationship between variables is very important. Since mathematics is a part of every natural science, it is also important in them. The relationship can be directly perpendicular or indirectly perpendicular or not perpendicular at all. Teaching it to every student in elementary or secondary school is hard. The constant difference can make it very easy and simple.
For example, think you want your student to understand the relationship between the change of distance of an object in a unit of time with the speed of the object. This can be done easily by using Constance difference. Since the time is 1 if we increase speed by some amount the distance will increase by the same amount. So the change of distance of an object in a unit of time is proportional to the speed of the object.
More about learning strategies.
We’re going to cover several different topics including the development of basic skills and classroom teaching strategies now. We’re going to begin this with a broad overview of mathematics instructions. The research has shown the effectiveness of early start programs young students are better prepared and have improved opportunities for success when learning mathematics at an early age. Research also demonstrates the significance of the classroom teacher on the success of the child.
Ineffective classroom teachers can seriously hinder a child’s academic growth in mathematics. Explicit systematic instruction is considered to be one of the most effective methods of teaching mathematics. Teachers model skills guide students on that skill and check for understanding teachers should emphasize maths priority standards. Priority standards are your must-know standards needed for mastery to advance to the next grade level.
For mathematics, instruction assessment of student performance is necessary for instruction. Just as it is providing feedback due to the number of different skills in a given mathematics curriculum, it is essential for classroom teachers to frequently check for understanding to ensure that they aren’t moving too fast. Also, those students aren’t falling behind.
Using these mathematical strategies, a student can have a better understanding about what are these concepts and their applications. I hope now you understand what is the constant difference and why it is important. Stay with us for more articles.


